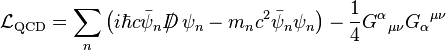|
Some details for Foundations of cosmology ANIL MITRA, COPYRIGHT © FEBRUARY 2016 – June 2017 Contents General relativity: field equations Quantum theory: some equations
Some details for roundations of cosmology General relativity: field equationsWith thanks to Wikipedia.
Gμν is symmetric:
where gμν is the metric tensor. The curvature scalar
The Ricci tensor, Rμν is related to the more general Riemann curvature
Tμν is the energy momentum tensor. Quantum theory: some equationsWith thanks to Wikipedia. Schrödinger:
Klein-Gordon
Dirac: Lorentz Invariant form
Pauli
Quantum electrodynamicsThe Lagrangian for a spin-1/2 field interacting with the electromagnetic field is given by the real part of
where
e is the coupling constant, equal to the electric charge of the bispinor field; m is the mass of the electron or positron;
Quantum chromodynamicsThe Lagrangian density is:
D is the QCD gauge invariant derivative, n = 1 … 6, counts the quark types and Gαμν is the gluon field strength tensor. |